Ensemble Methods in Machine Learning: Bagging Versus Boosting
Jun 25, 2020 • 11 Minute Read
Introduction
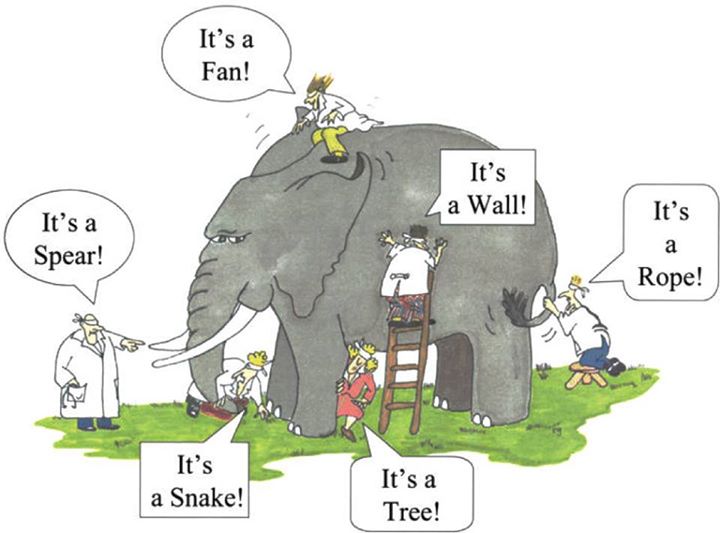
Ensemble methods* are techniques that combine the decisions from several base machine learning (ML) models to find a predictive model to achieve optimum results. Consider the fable of the blind men and the elephant depicted in the image below. The blind men are each describing an elephant from their own point of view. Their descriptions are all correct but incomplete. Their understanding of the elephant would be more accurate and realistic if they came together to discuss and combined their descriptions.
The main principle of ensemble methods is to combine weak and strong learners to form strong and versatile learners.
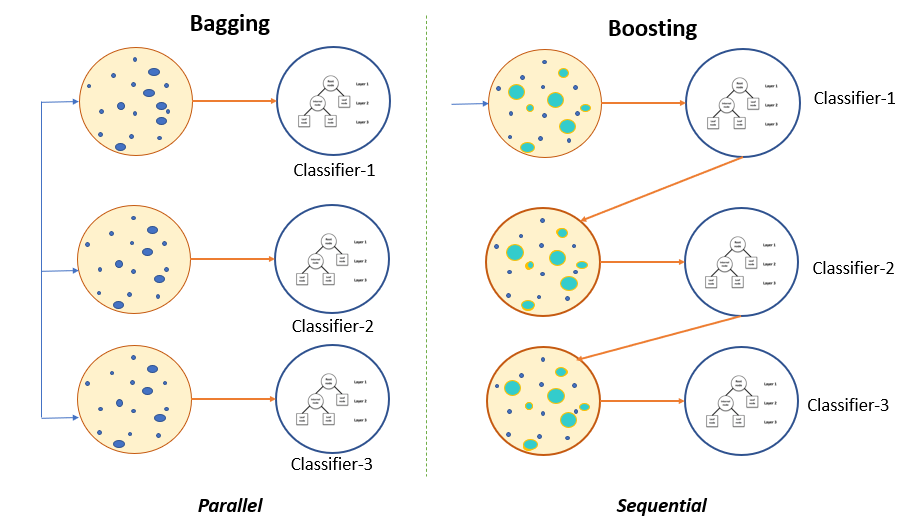
This guide will introduce you to the two main methods of ensemble learning: bagging and boosting. Bagging is a parallel ensemble, while boosting is sequential.
This guide will use the Iris dataset from the sci-kit learn dataset library.
But first, let's talk about bootstrapping and decision trees, both of which are essential for ensemble methods.
Bootstrapping
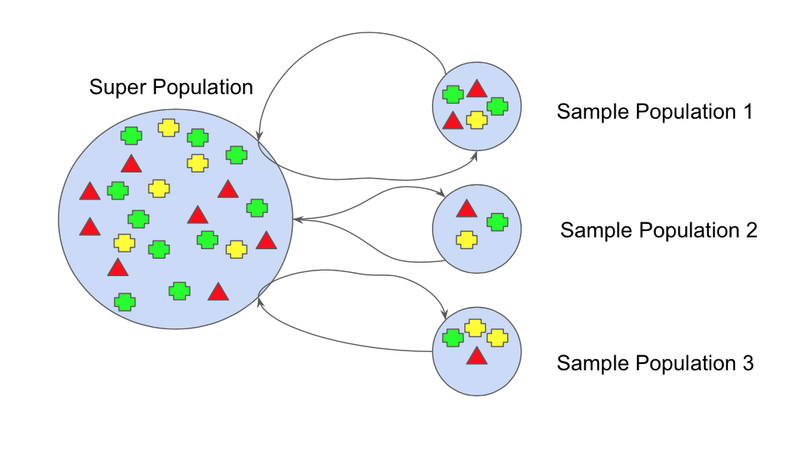
The bootstrap method refers to creating small multiple subsets of data from an entire dataset. These subsets of data are randomly sampled and replaced. The replacement of the sample is known as resampling.
Each section of the subsets will have equal probability. It will change the mean and standard deviation of the dataset, making the model more robust. The base learners and classifiers in the ensemble method will be mapped onto these subsets.
Decision Trees
In machine learning, decision trees have a huge impact on decision-based analysis problems. They cover both classification and regression. As the name implies, they use a tree-like model containing nodes and leaves.
The decision tree below determines whether a person is fit or unfit.
In the above image, the model's root is at the top—it's an upside-down tree! Here, conditions are internal nodes and outcomes are leaf nodes.
Notice that the decision tree contains several if-else statements in a strict order, making the model inflexible. It gives rise to overfitting, which occurs when a function fits the data too well. That means the model will be accurate only on the data it's been trained on. The model fails to work if there is a slight change in the training data or new data.
Using one decision tree is can be problematic and might not be stable enough; however, using multiple decision trees and combining their results will do great. Combining multiple classifiers in a prediction model is called ensembling. The simple rule of ensemble methods is to reduce the error by reducing the variance.
Ensemble Techniques
In this section, you will learn about ensemble techniques including bagging and boosting.
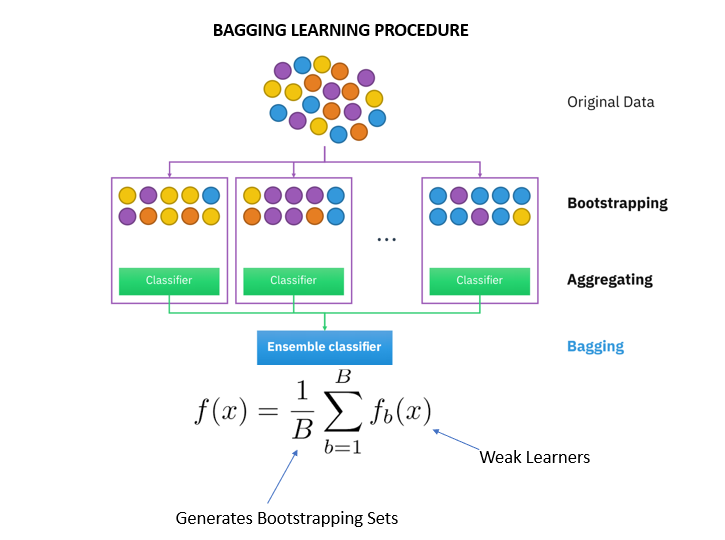
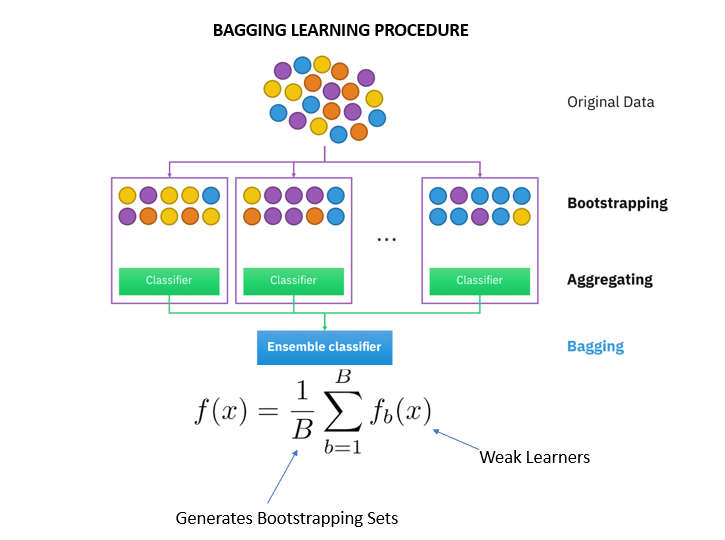
Bagging
The term "bagging" comes from the words Bootstrap Aggregator.
It fits the base learners (classifiers) on each random subset taken from the original dataset (bootstrapping). Due to the parallel ensemble, all of the classifiers in a training set are independent of each other so that each model will inherit slightly different features.
Next, bagging combines the results of all the learners and adds (aggregates) their prediction by averaging (mean) their outputs to get to final results.
The Random Forest (RF) algorithm can solve the problem of overfitting in decision trees. Random orest is the ensemble of the decision trees. It builds a forest of many random decision trees.
The process of RF and Bagging is almost the same. RF selects only the best features from the subset to split the node.
The diverse outcomes reduce the variance to give smooth predictions.
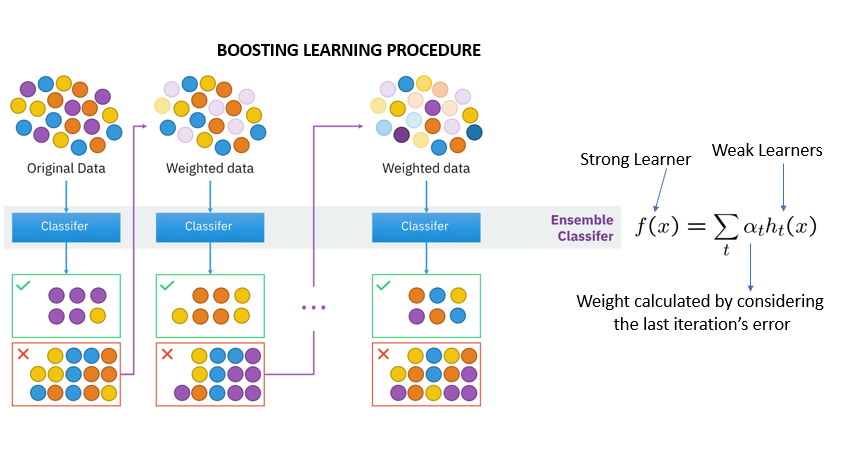
Boosting
The boosting technique follows a sequential order. The output of one base learner will be input to another. If a base classifier is misclassified (red box), its weight will get increased (over-weighting) and the next base learner will classify more correctly.
The next logical step is to combine the classifiers to predict the results.
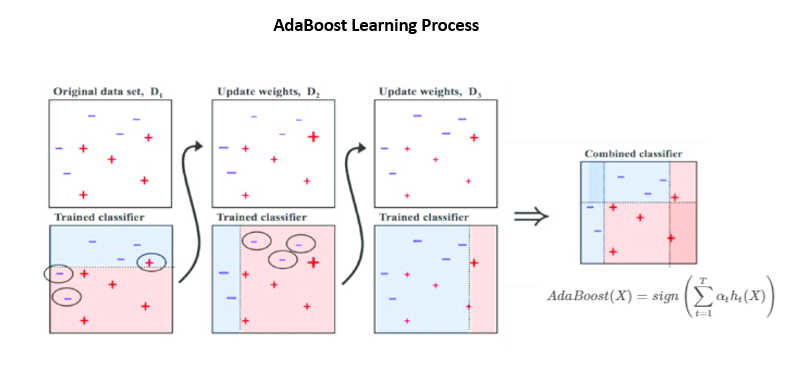
Gradient Descent Boosting, AdaBoost, and XGbooost are some extensions over boosting methods.
Gradient boosting minimizes the loss but adds gradient optimization in the iteration, whereas Adaptive Boosting, or AdaBoost, tweaks the instance of weights for every new predictor.
Boosting—or any other ensemble method, for that matter—will reduce the likelihood of overfitting of the model.
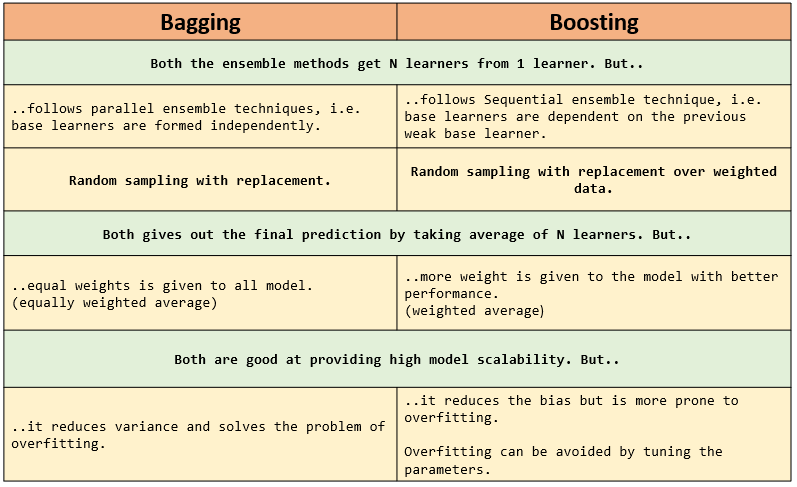
Comparing Bagging and Boosting
The table below shows the similarities and the differences between the ensemble methods.
Time to implement the code.
Code Implementation
The main drivers of building the classifier model are Sci-Kit Learn's sklearn.tree and sklearn.ensemble.
Before starting the classifier implementation, it is important to call the Decision Tree from sklearn.tree. Only then will the sklearn.ensemble the function work. Read about the parameters of different ensemble methods here.
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier, BaggingClassifier, GradientBoostingClassifier,AdaBoostClassifier
from sklearn import datasets # import inbuild datasets
from sklearn.model_selection import train_test_split
from sklearn import metrics
from sklearn.model_selection import cross_val_score, cross_val_predict
from sklearn.metrics import confusion_matrix
Load the Iris data from ski-kit learn datasets.
iris = datasets.load_iris()
X = iris.data
y = iris.target
The next step is to split the data set into 70% training and 30% testing using the hold-out method.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
Decision Tree
Initialize the score as it will help you check whether the model is overfitting. A standard process to implement any classifier model is calling the classifier function, fitting the classifier on training data and target data, and finally predicting outcomes on X_test.
score=[]
classifier = DecisionTreeClassifier()
classifier.fit(X_train, y_train)
classifier.score(X_train, y_train),classifier.score(X_test, y_test)
(1.0, 0.9777777777777777)
Well, the test score seems good, but the 1.0 score shows the model is overfitting!
Ensemble models to the rescue!
Bagging: Random Forest
rf = RandomForestClassifier(n_estimators=100)
bag_clf = BaggingClassifier(base_estimator=rf, n_estimators=100,
bootstrap=True, n_jobs=-1,
random_state=42)
bag_clf.fit(X_train, y_train)
bag_clf.score(X_train,y_train),bag_clf.score(X_test,y_test)
(0.9904761904761905, 0.9777777777777777)
The accuracy is around 98%, and the model solves the problem of overfitting. Amazing!
Let's check boosting algorithms before predicting the species.
Boosting: Gradient Boosting
Sci-kit learn's gradient boosting defaults to the decision tree only. Hence, it is also known as Gradient Boosting Decision Tree.
gb = GradientBoostingClassifier(n_estimators=100).fit(X_train, y_train)
gb.fit(X_train, y_train)
gb.score (X_test,y_test),gb.score (X_train,y_train)
(0.9333333333333333, 1.0)
It is overfitting! Same as with the decision tree. Let's check the situation with AdaBoost.
Boosting: AdaBoost
ad = AdaBoostClassifier(n_estimators=100, learning_rate=0.03)
ad.fit(X_train, y_train)
ad.score(X_train, y_train), ad.score(X_test, y_test)
(0.9619047619047619, 0.8666666666666667)
Well! The model doesn't overfit, but the test score is not as good as what RF gives.
Predict the target species using the RF classifier.
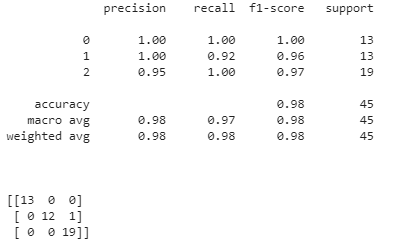
y_pred=bag_clf.predict(X_test)
print(classification_report(y_test,y_pred))
print('\n')
print(confusion_matrix(y_test,y_pred))
Conclusion
So, is bagging better than boosting?
Well, there is no clear winner. It depends on the data and problem statement. Finding a trade-off between variance and bias is necessary to have good results. If the model is performing great on training data but not on test data, then there’s a huge variance that needs to be dealt with. Similarly, if the model is not learning enough on training data, it cannot be used for generalization.
I recommend playing around with your dataset and seeing the changes in the test data score that happen when you tune the parameters. You can also experiment with different ensembles like XGBoost.
Feel free to contact me for help with any machine learning projects.
Advance your tech skills today
Access courses on AI, cloud, data, security, and more—all led by industry experts.